公元1858年，德国数学家莫比乌斯（Mobius，1790～1868）和约翰·李斯丁发现：把一根纸条扭转180°后，两头再粘接起来做成的纸带圈，具有魔术般的性质。普通纸带具有两个面（即双侧曲面），一个正面，一个反面，两个面可以涂成不同的颜色；而这样的纸带只有一个面（即单侧曲面），一只小虫可以爬遍整个曲面而不必跨过它的边缘。这种纸带被称为“莫比乌斯带”（也就是说，它的曲面从两个减少到只有一个）。

命名来源

公元1858年，德国数学家莫比乌斯（Mobius，1790～1868）和约翰·李斯丁发现：把一根纸条扭转180°后，两头再粘接起来做成的纸带圈，具有魔术般的性质。普通纸带具有两个面（即双侧曲面），一个正面，一个反面，两个面可以涂成不同的颜色；而这样的纸带只有一个面（即单侧曲面），一只小虫可以爬遍整个曲面而不必跨过它的边缘。这种纸带被称为“莫比乌斯带”（也就是说，它的曲面从两个减少到只有一个）。

概念描述

莫比乌斯带是一个二维的紧致流形（即一个有边界的面），可以嵌入到三维或更高维的流形中。这个带子本身是个二维概念，但它的扭曲是个三维动作，把二维材料施加三维动作，那它就是个三维物体概念了。莫比乌斯带严格意义上讲不是穿越了边界来到了反面，而是这个带子本身的表面就是个整体，是一面。一个莫比乌斯带沿边界粘上一个圆盘就得到二维实射影空间，两个莫比乌斯带沿边界粘起来就得到一个克莱因瓶。

莫比乌斯带的重要特性是：虽然在每个局部都可以说正面反面，但整体上不能分隔成正面和反面，即这种曲面是只有一个面的 “单侧曲面”。

引申意义

可能莫比乌斯环在每个人心中的意义都不同，如下是摘自知乎一位匿名用户的回答，是不是觉得还蛮有意思呢!

理想爱情。

• 如果某个人站在一个巨大的莫比乌斯带的表面上沿着他能看到的“路”一直走下去，他就永远不会停下来。
• 数学家断言：莫比乌斯带只有一边。如果你不相信，就请剪开一个验证，带子分离时候却还是相连。

三维建模

下图是我用Solidworks绘制的莫比乌斯环，直接来看是由三个莫比乌斯带沿边线两两粘合而成的，提供下载链接，大家可以自己尝试呀！

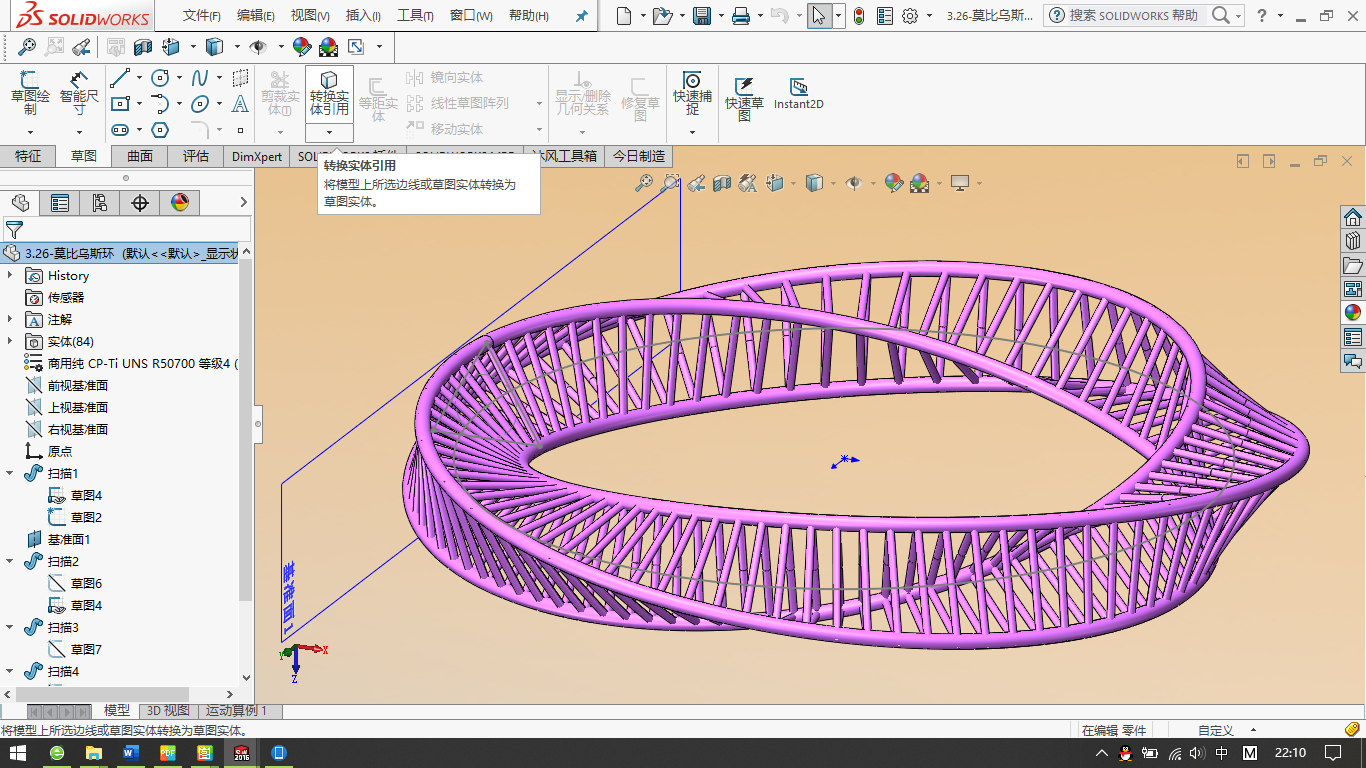
（本文部分图片源自网络，如侵删）
莫比乌斯环SW模型下载 (opens new window)

每日歌曲分享之《烟笼长安》

岁月不堪数，故人不知处。最是人间留不住，三千红尘路，长安故土。